探究发现教学模式的设计思路

一、关于教学内容和要求的思考

本节课是在课本“四边形”这一章中介绍完特殊的平行四边形──矩形、菱形、正方形之后的一节探究课。具体教学内容是：课前学生通过上网、查阅资料等方式了解哥尼斯堡的七桥问题，体会转化的数学思想在解决实际问题中的重要性。同时学生利用图形计算器体验一个数学上的发现（任意四边形的中点四边形是平行四边形这一简单而美观的结论），通过教师的适当引导，学生投人探究中点四边形为什么是平行四边形这一活动中，通过这个探究活动来体验知识的获得过程。学习欧拉解决七桥问题的思想方法，从而把一个四边形的问题转化成一个三角形问题。在问题的转化与解决过程中生成了三角形中位线定理。最后，学生利用发现的定理展开新一轮的探究，在整个教学过程中，学生经历了提出问题──观察──猜想──证明──问题解决的科学探索过程，探究式教学贯穿于始终。尽管学生在探究过程中也曾体验失败，但最终他们体会到的是解决问题的快乐。

对中点四边形性质的认识以探究的形式展开，我们的想法主要有以下几点：一是强调学生对研究过程的参与以及对科学概念、科学方法、科学态度的掌握或形成为目标的探究教学已成为实施新课程的一种基本教学模式。对四边形的中点四边形性质的认识过程实际上也是三角形中位线定理的生成过程，学生通过对中点四边形性质的探究使得他们对三角形中位线定理的生成有了科学的理解，这种理解是建立在自主探究的基础之上的，而不是被动的接受。二是探究式教学应该使探究的问题具有适度的探究空间和潜在的距离。从一个四边形的问题到一个三角形问题，学生经历了由一个问题向另一个问题逐渐转化的过程，这实际上是一个科学的探索过程。同时，新课程强调课堂教学应该以学生为主体，如何体现这一主体？我们的看法是在教学过程中应该充分体现数学的教学活动，而数学教学活动的核心是数学思维活动，应该让学生学会用数学的方法去思考一些问题。在解决中点四边形是平行四边形这一过程中，问题不断向问题转化，图形也随之逐渐简化，这种转化与简化实际上是一种较高层次的数学思维过程的体现，在课堂上应该得到充分的展示。

此外学生在利用图形计算器进行探究的过程中，随着原四边形一顶点的拖动，原四边形可能将不再是学生较为熟悉的凸四边形，而有可能是凹四边形或折四边形，关于凹四边形或折四边形，课本中没有编写相关方面的知识，但我们认为对凹四边形或折四边形的中点边形的探究不应该回避，我们应该给学生一个较为完整的认识体系。实际上凸四边形的中点四边形的特点对凹四边形或折四边形而言都是一样的。对学有余力的学生，在完成对凸四边形的中点四边形的探究后，研究凹四边形或折四边形的中点四边形是可以接受的。这样一方面提高了学生的认识，培养了学生由特殊到一般的认识事物的能力；另一方面巩固学生对刚学习的三角形中位线定理的认识。

二、关于教学目标、重难点的确定

根据课程标准的要求和教学内容的特点，针对学生的学习水平，确定本节课的教学目标如下：

知识与技能 学会利用已经掌握的数学知识猜想、探索未知的数学知识，在探索的过程中学会将数学问题进行转化。

过程与方法 体验从问题出发，观察──猜想──证明──问题解决的科学探索过程，体会探索的过程实际上就是一个问题的转化过程。

情感态度价值观 学会自主探究、多视角的分析问题，感受在探索过程中发现三角形中位线定理的快乐，学会与人合作交流。

由以上目标确定的教学重点是在探索过程中如何实现问题与问题间的转化，教学难点是找出研究问题的本质，在四边形中分离出三角形。

三、关于教学过程的设计及其思考

整个教学程序是这样的：课前学生通过上网、查阅资料等方式了解哥尼斯堡的七桥问题，学生体会转化的数学思想在解决实际问题中的重要性。同时学生利用图形计算器体验数学发现（任意四边形的中点四边形是平行四边形），然后，在解释为什么时，遇到了挑战，用一些常规的方法在这里难以奏效，于是必须从特殊的视角来分析和解决这个问题。在教师的引导下学生开始尝试对研究的问题进行转化，在问题转化的同时对图形也进行相应的简化通过学生的自主探究和教师的适当介人。引导学生发现解决这个问题的关键是要研究三角形中两条特殊线段之间的关系，在研究这两条特殊线段间的位置关系和数量关系后，发现了三角形中位线定理。接着教师提出新的问题，学生利用新发现的定理展开新一轮的探究。整个教学过程围绕着提出问题──观察──猜想──证明──问题解决—解决新问题这一过程展开。

具体的教学过程分为：（1）创设情境（提出问题）；（2)中点四边形性质探究（解决问题）；(3）对中点四边形的进一步探究（提出新问题并解决新问题）；（4)课堂小结共四个阶段。

1、创设情境

情境1 哥尼斯堡七桥问题。课前学生通过上网、查阅资料等方式了解了哥尼斯堡七桥问题。教师则点明为什么欧拉能够解决七桥问题：关键是欧拉没有在原来的情境当中研究该问题，而是把七桥问题中的四块陆地抽象成四个点，七座桥抽象成七条线，从而使七桥问题转化成一个一笔画问题，这个一笔画问题解决了，哥尼斯堡七桥问题也就解决了。转化思想在问题的解决中起了至关重要的作用，这也是探究中点四边形性质的一个重要思想方法。

情境2 四边形的中点四边形问题。教师提出任务：让学生利用图形计算器画一个任意四边形，依次连接各边中点，所得到的新四边形为中点四边形，让学生拖动原四边形的其中一个顶点，改变原四边形的形状，观察图形的变化过程，看看有什么发现。一名学生回答并进行了演示：拖动原四边形的一顶点，改变原四边形的形状，发现中点四边形是平行四边形。如何解释这一发现呢？──提出问题。

2、中点四边形性质探究

（1)探究过程中的问题转化

教师提问：大家是如何得到这一发现的呢？学生回答是通过观察发现中点四边形的两组对边分别平行，故猜测中点四边形是平行四边形。由观察到猜想，符合学生对事物的认知规律，这也是科学探索的步骤之一在学生获得猜想后，教师进行适度的引导：实际上我们找到了一种证明中点四边形是平行四边形的思路

原问题可转化为：证明中点四边形的两组对边分别平行。一学生根据图形的特点指明只需要证明一组对边互相平行就可以了，因为另一组对边平行的结论可以同理可证。这样原问题又在向新的一个问题转化。如何证明中点四边形的一组对边互相平行呢？学生开始回顾判定两直线互相平行的方法，并利用图形计算器进行探究。很快学生发现利用同位角、内错角、同旁内角的关系来证明比较困难，教师提醒学生是否能利用其他的办法来证明一组对边互相平行。一学生回答：可以利用“平行于同一条直线的两直线互相平行”来证明。接下来，问题转化成如何寻找这条“中介”直线。学生开始利用图形计算器进行探究。请一名学生上讲台演示其发现的过程，指明BD就是我们要寻找的“中介”直线。教师追问此时我们研究什么问题就可以解决原问题。让学生体会到命题的证明过程实际上也是命题的转化过程，是一个从未知逐步转化到已知的过程，让学生逐步体会到“转化”的数学思想方法在分析问题中的重要作用。

(2）探究过程中的图形转化

提醒学生注意欧拉在研究七桥问题时是把问题逐步进行转化，图形也进行相应的简化，最终才解决七桥问题。图形的转化与简化最终也是解答七桥问题的重要因素。我们也应学习数学家的这一思想方法来解决现有问题。引导学生发现要研究GF与BD间的位置关系，只需要在中研究就可以了。所以可以把从四边形ABCD中分离出来，在三角形中研究GF与BD间的位置关系就可以了。这样问题与图形都得到了关键性的转化和简化。由四边形问题转化成三角形问题，这是问题得到解决的关键性一步，命题得到了进一步的简化，从而由对中点四边形性质的探究转人到对三角形中两条线段位置关系的探究。

(3)三角形中位线定理的发现

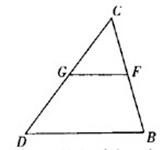
提出任务：如图，在中，G、F分别是CD,CB的中点。证明：GF／／ BD 学生画图、分析、求证。一学生阐述自己的证明思路，教师板书。证明完毕后，原问题获得了圆满的解决。我们得到了一个结论：四边形的中点四边形是平行四边形。在这一问题中，我们得到了GF与BD间的位置关系，那么它们之间是否存在确定的数量关系呢?学生很快做出正确的回答。教师说明线段GF的特点（两个端点分别是三角形两边中点），引出三角形中位线定义和三角中位线定理。

3、对中点四边形的进一步探究

在对中点四边形性质进行探究的过程中，随着原四边形顶点的拖动，原四边形的形状会发生相应的变化，将有可能不再是我们常见的凸四边形，而有可能是凹四边形或折四边形（如图所示）。这种变化在学生的操作中是不可避免会出现的，为了开拓学生的视野，使学生对任意四边形的任意性有一个更为全面的认识，同时加强对三角形中位线定理的理解和应用。设计了拓展1，即四边形ABCD是凹四边形或折四边形时。原结论是否还成立？

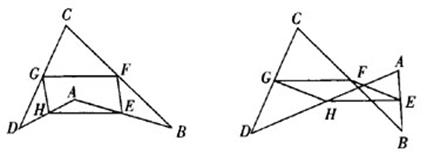
学生争先恐后轻松地解决了这个问题。

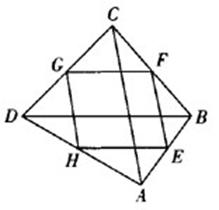
通过上一问题，学生对四边形ABCD形状的任意性有了一个新的认识：不管四边形ABCD是凸四边形、凹四边形，还是折四边形，其中点四边形EFGH都是平行四边形，但是四边形EFGH有没有可能是一些特殊的平行四边形呢？回答是肯定的。为此设计拓展2:当中点四边形EFGH为菱形时，原四边形ABCD应该满足什么条件？学生对这一问题马上产生浓厚的兴趣，展开新一轮的探究。设计拓展2的主要目的是促使学生进行逆向思维，升华定理的应用。经过几分钟的思考和对图形计算器的操作，一学生上来演示了他的操作过程，他利用了几何画板中对线段长度的测量工具完成了这一探究过程：测量GF, GH的长度，拖动A点改变四边形ABCD的形状，使得GF=GH，得到中点四边形GFEH为菱形。测量此时BD,AC的长度，发现BD=AC.利用刚学习的三角形中位线定理解释这一发现，从而得到结论：当四边形的对角线相等时，其中点四边形是菱形。该同学的操作和发言得到老师和同学们的充分肯定。那么，当中点四边形是其他特殊的平行四边形如矩形、正方形时，原四边形又应当满足什么条件呢？这一探究课题留给学生课后去思考完成。

4、课堂小结

师生共同小结：（l）结合本节课，你觉得一个科学的探索过程应该怎样来进行？（2)本节课对你今后的学习有何启发？课堂小结是对整节课的知识体系作一个较为全面的回顾，体会其中的科学探索过程，激发学生对知识的求知欲。