透视数学中考中应用建模题

这类问题在解决时，首先要在阅读材料、理解题意的基础上，把实际问题抽象为数学问题，即将实际问题经过抽象概括，利用数学知识建立相应的数学模型。再利用数学知识对数学模型进行分析、研究，从而得出结论。然后再把解得的数学结论返回到实际问题中。下面分类予以说明：

一、建立数式模型

数与式是最基本的数学语言，由于它能有效、简捷、准确地揭示由低级到高级、由具体到抽象、有特殊到一般的数学思维过程，富有通用性和启发性，数与式模型通常成为学生抽象和概括数学问题的重要方法。

例1　（2004年安徽芜湖市中考题）小王上周五在股市以收盘价（收市时的价格）每股25元买进某公司股票1000股，在接下来的一周交易日内，小王记下该股票每日收盘价格相比前一天的涨跌情况：（单位：元）

根据上表回答问题：

①星期二收盘时，该股票每股多少元？

②周内该股票收盘时的最高价，最低价分别是多少？

③已知买入股票与卖出股票均需支付成交金额的千分之五的交易费。若小王在本周五以收盘价将全部股票卖出，他的收益情况如何？

解：（1）星期二收盘价为25＋2－0.5＝26.5（元/股）

（2）收盘最高价为25＋2－0.5＋1.5＝28（元/股）

收盘最低价为25＋2－0.5＋1.5－1.8＝26.2（元/股）

（3）小王的收益为：27×1000（1－5‰）－25×1000（1＋5‰）

＝27000－135－25000－125

＝1740（元）

∴小王的本次收益为1740元。

二、建立方程（组）模型

方程（组）是研究现实世界数量关系的最基本的数学模型，求解此类问题的关键是：针对给出的实际问题，设定合适的未知数，找出相等关系，但要注意验证结果是否适合实际问题。

例2　（2004年山东省枣庄市中考题）某家庭新购住房需要装修，如果甲、乙两个装饰公司合做，12天可以完成，需付装修费1.04万元；如果甲公司先做9天，剩下的由乙公司来做，还需16天完成，共需付装修费1.06万元。若只选一个装饰公司来完成装修任务，应选择哪个装饰公司？试说明理由

解：设甲公司单独做x天完成，乙公司单独做y天完成。根据题意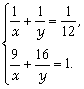，得解之，得。

经检验，是原方程组的解，且符合题意。

设甲公司单独完成装修工程需装修费a万元，乙公司单独完成装修工程需装修费b万元。则

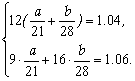解之，得

所以，甲公司完成装修工程需21天，装修费0.98万元；乙公司完成装修工程需28天，装修费1.12万元。从节约时间、节省开支的角度考虑，应选择甲公司来完成此项装修任务。

三、建立不等式模型

现实世界中不等关系是普遍存在的，许多现实问题很难确定（有时也不需要确定）具体的数值。但可以求出或确定这一问题中某个量的变化范围，从而对所有研究问题的面貌有一个比较清楚的认识。

例3　（2004年河北省中考题）光华农机租赁公司共有50台联合收割机，其中甲型20台，乙型30台。先将这50台联合收割机派往A、B两地区收割小麦，其中30台派往A地区，20台派往B地区。

两地区与该农机租赁公司商定的每天的租赁价格见下表：

（1）设派往A地区x台乙型联合收割机，租赁公司这50台联合收割机一天获得的租金为y（元），求y与x间的函数关系式，并写出x的取值范围；

（2）若使农机租赁公司这50台联合收割机一天获得的租金总额不低于79600元，说明有多少种分配方案，并将各种方案设计出来；

（3）如果要使这50台联合收割机每天获得的租金最高，请你为光华农机租赁公司提一条合理化建议。

解：（1）若派往A地区的乙型收割机为x台，则派往A地区的甲型收割机为（30－x）台；派往B地区的乙型收割机为（30－x）台，派往B地区的甲型收割机为（x－10）台。

∴y＝1600x＋1800（30－x）＋1200（30－x）＋1600（x－10）＝200x＋74000

x的取值范围是：10≤x≤30（x是正整数）

（2）由题意得200x＋74000≥79600

解不等式得x≥28由于10≤x≤30（x是正整数）

∴x取28，29，30这三个值。

∴有3种不同的分配方案。

①当x＝28时，即派往A地区的甲型收割机为2台，乙型收割机为28台；派往B地区的甲型收割机为18台，乙型收割机为2台。

②当x＝29时，即派往A地区的甲型收割机为1台，乙型收割机为29台；派往B地区的甲型收割机为19台，乙型收割机为1台。

③当x＝30时，即30台乙型收割机全部派往A地区；20台甲型收割机全部派往B地区。

（3）由于一次函数y＝200x＋74000的值y是随着x的增大而增大的，所以当x＝30时，y取得最大值。如果要使农机租赁公司这50台联合收割机每天获得租金最高，只需x＝30，此时，y＝6000＋74000＝80000。

建议农机租赁公司将30台乙型收割机全部派往A地区；20台甲型收割机全部派往B地区，可使公司获得的租金最高。

四、建立函数模型

函数应用问题涉及的知识层面丰富，解法灵活多变，是考试命题的热点问题。解答此类问题，一般都是从建立函数关系入手，将实际问题模型化或结合函数图象来挖掘解题思路。

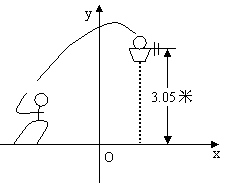
例4　（2004年安徽南山区中考题）如图，一位篮球运动员跳起投篮，球沿抛物线运行，然后准确落入篮框内。已知篮框的中心离地面的距离为3.05米。

（1）球在空中运行的最大高度为多少米？

（2）如果该运动员跳投时，球出手离地面的高度为2.25米，请问他距离篮框中心的水平距离是多少？

解：（1）∵抛物线的顶点坐标为（0，3.5）

∴球在空中运行的最大高度为3.5米

（2）在中

当y＝3.05时x＝±1.5又 ∵x＞0 ∴x＝1.5

当y＝2.25时x＝±2.5又 ∵x＜0 ∴x＝－2.5

故运动员距离篮球中心水平距离为｜1.5｜＋｜－2.5｜＝4米

五、建立统计模型

统计知识在现实生活中有着广泛的应用，作为学生要学会深刻理解基本统计思想，要善于提出问题，考虑抽样，收集数据，分析数据，做出决策，并能进行有效的交流、评价与改进。

例5　（2004年福建省南平市中考题）下图反映了被调查用户对甲、乙两种品牌空调售后服务的满意程度（以下称：用户满意程度），分为很不满意、不满意、较满意、很满意四个等级，并依次记为1分、2分、3分、4分。

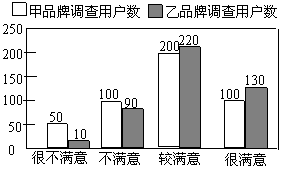
（1）求甲、乙两品牌用户满意程度分数的平均值；（计算结果保留到小数点后第2位）

（2）根据条形统计图及上述计算结果说明哪个品牌用户满意程度较高？该品牌用户满意程度分数的众数是多少？

（1）甲品牌被调查用户数为50+100+200+100＝450（户）

乙品牌被调查用户数为：10+90+220+130＝450（户）

甲品牌满意程度分数的平均值＝（分）

乙品牌满意程度分数的平均值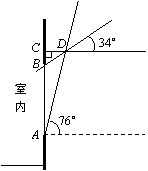＝（分）

答：甲、乙两品牌用户满意程度分数的平均值分别为2.78（分），3.04（分）

（2）用户满意程度较高的品牌是乙品牌

因为乙品牌满意程度分数的平均值较大，且由统计图，乙品牌“较满意”、“很满意”的用户较多。

该品牌用户满意程度分数的众数是3。

六、建立几何模型

几何应用题内容丰富，诸如测量、取料、剪裁、方案设计、美化设计等等。解答此类问题的一般方法是认真分析题意，把实际问题进行抽象转化为几何问题，进而运用数学知识求解。

例6　（2004年淄博市中考题）在日常生活中，我们经常看到一些窗户上安装着遮阳蓬，如图（1）。现在要为一个面向正南的窗户设计安装一个遮阳蓬，已知该地区冬天正午太阳最低时，光线与水平线的夹角为34°；夏天正午太阳最高时，光线与水平线的夹角为76°。

把图①画成图②，其中AB表示窗户的高，BCD表示直角形遮阳蓬。

（1）遮阳蓬BCD怎样设计，才能正好在冬天正午太阳最低时光线最大限度地射入室内而夏天正午太阳最高时光线刚好不射入室内？请在图③中画图表示；

（2）已知AB＝150cm，在（1）的条件下，求出BC，CD的长度（精确到1cm）。

解：（1）如图。

（2）如图，设BC＝x，CD＝y。在Rt△ADC和Rt△DBC中，

由题意，得把②代入①，得，

（cm），

（cm）。

答：BC、CD的长度分别约为30cm、45cm。

七、建立线性规划模型

近年来，中考试题中开始出现线性规划问题。所谓线性规划，是指求线性函数在线性（不等式或等式）约束下达最（小或大）值的问题。线性规划广泛应用于工农业、军事、交通运输、决策管理与规划、科学实验等领域。

例7　（2004年山东省烟台市）先阅读下面的材料，然后解答问题：

在一条直线上有依次排列的n（n＞1）台机床在工作，我们要设置零件供应站P，使这n台机床到供应站P的距离总和最小，要解决这个问题，先退到比较简单的情形：

如图①，如果直线上有2台机床时，很明显设在A₁和A₂之间的任何地方都行，因为甲和乙走的距离之和等于A₁到A₂的距离。

如图②，如果直线上有3台机床时，不难判断，供应站设在中间一台机床A₂处最合适，因为如果P放在A₂处，甲乙和丙所走的距离之和恰好为A₁到A₃的距离，而如果把P放到别处，例如D处，那么甲和丙所走的距离之和仍是A₁到A₃的距离，可是乙还得走从A₂到D的这一段，在是多出来的，一次P放在A₂处是最佳选择。

不难知道，如果直线上有4台机床，P应设在第2台与第3台之间的任何地方；有5台机床，P应设在第3台的位置。

问题（1）：有n台机床时，P应设置在何处？

问题（2）：根据问题⑴的结论,求︱x－1︱+︱x－2︱+︱x－3︱+…+︱x－617︱的最小值。

解：（1）当n为偶数时，P应设在第台和（＋1）台之间的任何地方，

当n为奇数时，p应设在第台的位置。

（2）根据绝对值的几何意义，求︱x－1︱+︱x－2︱+︱x－3︱+…+︱x－617︱的最小值就是在数轴上找出表示x的点，使它到表示1，2，…，617各点的距离之和最小，根据问题1的结论，当x＝309时，原式的值最小。

最小值是：︱309－1︱+︱309－2︱+︱309－3︱+…+︱309－308︱+0+︱309－310︱+︱309－311︱+…+︱309－311︱＋+︱309－616︱+︱309－617︱＝308＋307＋306＋…＋1＋1＋2＋…＋308＝308×309＝95172。

总之，这类问题透视热点，力求创新，将是今后中考命题的趋势。希望同学们在日常的学习过程中，掌握建模的方法、规律，切实提高自己解决实际问题的能力。