试论灵活设问与创造性思维的培养

关键词：设问，创造性思维，发散思维

最新颁布的数学新课程标准要求教师要“通过研究性、探究性的学习，培养学生具有创新能力、实践能力和终生学习的能力”。其中，创新能力的培养应是培养目标中的核心。而创新能力的培养中，创造性思维的培养又是核心中的核心。

所谓创造性思维，是指有创建的思维，即通过思维，不但能揭示客观事物的本质及其内在联系，而且在此基础上能产生新颖的、前所未有的思维成果。它是智力水平高度发展的产物，是后天培养与训练的结果。创造性思维以新颖独特的方法解决问题，具有发散性和收敛性、灵活性和多变性、独特性和新颖性的特点。

在研究性学习过程中，鼓励教师在教学中“要提倡灵活多样的教学方式，尤其是采用启发式和讨论式的设问，充分发展学生的个性，发展其思维能力，激发想象力和创造潜能”，“避免烦琐的分析和琐碎机械的练习”。可见，灵活巧妙的设问，不仅具有活跃课堂气氛的功能，更具有培养学生创造性思维的作用。

通过以上对设问和创造性思维的理解和界定，可以看出，在数学教学中，教师通过课堂的灵活设问，对培养学生的发散思维和集中思维，启迪直觉思维，培养创造机智等具有重要的意义。

1 、 创设良好的课堂氛围和设问情境，为灵活设问的效能最大化创造前提

我国的传统教育比较注重学生求同思维的养成，往往容易忽视对学生求异品质的塑造。因此，我们在课堂教学中，应充分利用一切可供想象的空间，充分发挥学生的想象力，培养学生的创造力。

具体而言，我们要提倡建立“畅所欲言，各抒己见”的课堂氛围，为学生提供独立活动、自我表现的机会和条件；应鼓励学生对老师的提问产生质疑，能够提出自己不同的观点和看法；应鼓励学生由此及彼，从一个问题衍生开来，提出崭新的、有创造性的问题。只有这样，教师的设问才会最大可能地激发学生的创造性思维。

要鼓励学生拥有坚持己见的自信和勇气，引导学生为证明自己的观点找证据，求事实；但同时应引导学生既要敢于坚持己见，又要善于接纳别人正确的观点，从而在对某个问题的讨论中获得最大收益。

要创设合适的问题情境，激发学生探讨数学问题的兴趣。学习兴趣和求知欲是学生能否积极思维的动力。在数学问题情境中，新知识的需要与学生原有的数学水平之间存在着认识冲突，而这种冲突正是诱发学生数学思维的积极性和创造性所必需的。

例如： 对于分式的化简，就可设计如下的诱发过程以引导学生：

大多数学生对分式的加减运算都懂得先通分后加减，但这一方法对本题不适用，教师可问学生能否用其它方法对它进行化简。譬如，分别观察分式的分子、分母，寻找形式上的特点。通过教师这一引导性的提问激发起了学生的兴趣，学生的思维便活跃起来，积极对该式进行观察、分析。原来 ：可化为；可化为，从而达到了化简的目的。

2. 多角度、多层次、多方位设问，培养学生发散思维

发散思维是创造性思维的主导成分，又是创造性思维的核心，它着眼于探索未知的事物，发现事物间的新关系，寻找多方面解决问题的方法。因此，将一个问题从不同角度、不同层次进行设问，也可训练学生的发散思维，进而培养学生的创造性思维。具体而言，思考问题时，根据同一来源材料，以比较丰富的知识为依托，沿着不同的方向去思考，以探求不同方向的解答，即通常所说的“一题多解”、“一题多变”。

又例：解方程

设问1：能否用换元法求解？

设，则，解得，然后求解；

设问2：能否根据方程特点，用一元二次方程求解？

可利用一元二次方程中“根与系数的关系”构造出一个一元二次方程，解得，然后求解；

设问3：能否构造倒数方程求解？

将原方程变为:

 ，然后直接求解。

3 .启发引导，保持创造性思维的持续性

在合适的问题情境中，学生思维的积极性被充分地调动起来，但应该怎样保持这种积极性，使其持续下去而不中断呢？

3．1 要给学生思考的时间

数学学习是通过思考进行的，没有学生的思考就没有真正的数学学习，思考问题是需要一定的时间的。值得研究的是，教师提出问题后，应该给学生多少思考时间。实验表明，思考时间若非常短，学生的回答通常也很简短，但若把思考时间延长一些，学生就会更加全面、较为完整地回答问题，这样，问题回答的准确率就会提高。当然，思考时间的长短，是与问题的难易程度和学生的实际水平密切相关的。目前，在课堂学习中，教师往往是提出问题后，几乎不给出思考时间，就要求学生立刻作答，而一旦学生不能立刻说出答案，教师便不断重复其问题，催促答案或者干脆另外提出一些问题来弥补这个"冷场"。其实，这恰恰是在干扰学生表面看似平静，实则活跃的思维过程。

3．2 教师启发要与学生的思维同步

教师提出问题后，一般应让学生先作一番思考，必要时教师可作适当的启发引导。教师的启发要遵循学生思维的规律，因势利导，循序渐进，不能强制学生按照教师提出的方法和途径去思考问题，喧宾夺主。 例如：初中学生在学习“三角形相似的判定”这一内容时，教师可选用如下的例题。

例：已知：如图1，△ABC 中，BE和CF是中线， 它们相交于点G，

求证：FG·CG = EG·BG

图 1

如果有的教师没有认真揣摩学生的思路，径直提出连结EF（图1），强行让学生证明△EFG∽△BCG。那么就可能脱离学生的实际，没能与学生的思维同步。有经验的教师往往“既备教材，又备学生”，在备课时认真揣摩学生的心理，估计课堂上可能发生的各种情况。对于这道例题，学生可能会去证明△BGF和△CGE相似，教师应让学生多讨论，去发现这两个三角形不一定相似，即使相似，也不符合本题结论的要求。如此一来，就为学生滤去了疑惑。此时，学生不须再启发，也会利用“点E、F分别为边AC、AB的中点”这一条件，进而联想到连结EF。

3．3 要不断向学生提出新的教学问题

问题不仅是教学的心脏、教学思维的动力，更是思维的方向。数学思维的过程就是不断地提出问题和解决问题的过程。因此，在数学课堂教学中，教师要及时地向学生提出新的数学问题，为更深入的数学思维活动提供动力和方向，使数学思维活动持续不断地向前发展。提出适当的数学问题必须符合下列条件：

3．3．1 问题要有方向性

这是指提问题要有明确的目的，要使学生的思维趋向于教学目标，否则，反倒会对学生产生误导。

3．3．2 问题的难度要适中

这是指问题不宜太难或太易，难易之间要有一定的梯度。教师提出的问题太难，学生“丈二金刚摸不到头脑”，则失去对问题进行分析的兴趣，更谈不上解决问题。相反，如果问题太简单，学生不费吹灰之力就得出答案，则其求知欲将降低，就会分散注意力，影响学习效果。所以，教师应针对不同层次学生的情况，分层次设问，分层次教学。

3．3．3 问题要有启发性

有的教师往往把启发式误认为提问式，认为问题提得越多越好。其实，问题并不在多，而在于是否具有启发性、是否是关键性的问题、是否能触及问题的本质，引导学生深入思考。

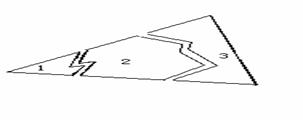
如上图：用一块打破成三块的三角形玻璃引入全等三角形的判定时，教师问：“若带碎片1去，带去了三角形的几个元素？若带碎片2去，带去了三角形的几个元素？若带碎片3去，带去了三角形的几个元素？”这就是个极为关键、富有启发性的问题，它引起了学生浓厚的兴趣，带动学生深入思考，并为学生学习应用“角边角公理”奠定了基础。

4．结论

总之，在课堂教学中，灵活巧妙的设问，对学生创造性思维的培养具有积极的意义。教师在教学过程中，不妨多采用，以达到更好的教学效果。

[参考书目]

[1] 中华人民共和国教育部 . 数学课程标准 . 北京：北京师范大学出版社 . 2002

[2] 教育部基础教育司 . 数学课程标准解读 . 北京：北京师范大学出版社 .2002

[3] 刘良慧，张先华 . 教育观念的革命 . 重庆 ： 重庆大学出版社 . 2000