传统的教学方法,就凭一张嘴、一支粉笔、一本书、一块黑板,仍至今天,尤其在我们农村中学,还有着极其强大的生命力。在这样的教学模式下,知识的掌握、难点和重点的突破,总是靠教师机械反复讲,学生机械反复的练。这样就导致了学生过重的课业负担,有的教师也百思不得其解,“这道题,我重复讲了五、六遍,还是不懂”,这恐怕不是挂在少数老师嘴上的口头禅。学生在学习的过程中总是在反复的识记、反复的再认和保持,要培养学生的创新思维,培养学生的实践能力,从何说起。那么要改变数学教学的这种状况,方法之一,就是利用学校现成的微机室,找一个适合学生的教学平台----几何画板,把它应用于教学之中。下面是笔者实践中的几点浅显的做法,它的最大作用,就是学生获益非浅,现说来与大家听听,只望能得到行家里手的指点。
一、 运用几何画板,使教师备课、制卷完美无缺
先前我备课、制卷都是用WORD2000,美中不足之处,就是难于处理几何图形,即使用“绘图”工具,但仍不能把图画准确。画一个确定的角、画角平分线、 平行线、垂线、三角形的内切圆、抛物线等,都不可能。有了几何画板,一切都那么轻松自如。我的备课笔记和制作的试卷,其中准确的几何图形、函数的图象等,总让人产生欲达无望的感觉。其实,只要你拥有几何画板,它就是你工作的得力助手。
二、 用几何画板揭示变化的图形中不变的几何规律
在进行圆一章中的相交弦定理、相交弦定理的推论、切割线定理、切割线定理的推论教学时,要想把它们归纳为圆幂定理,费尽心机,其效果也是很差。学生总是孤立地记忆,更不能灵活运用。但如果教学时,运用几何画板,则充分提示了变化的图形中不变的几何规律。
已知⊙O和点P,过P点作两条直线,分别和⊙O相交于A、B和C、D。利用几何画板,进行如下操作:(学生在微机室里,在教师的指导,自己进行操作。)

(一)当d、r不变时,拖动控制点1和控制点2,使弦AB、CD绕点P旋转,可得出相交弦定理。由于学生可以自己操作电脑,探索图形的性质,极大地调动了学生学习知识和探索规律的热情和主动性,也只有这样才能真正发挥学生的主体性。回味一下,我们在静态的黑板上,能达到这种效果吗?
(二)、当点P的位置不变,一条弦绕点P旋转经过圆心,另一弦旋转垂直于第一弦时,可以得出相交弦定理的推论

(三)、如果点P从圆内运动到圆外,可得割线定理

(四)、割线定理图形中的割线PCD绕点P旋转时,点C、D可以重合,且∠ODP=∠OCP=90o时,可得切割线定理。(课本中是先研究切割线定理,再研究割线定理,并把后者叫做切割线定理的推论,这里研究的顺序与课本不同,从图形之间的变化来考虑,这样做比较合理。)


(五)、 圆的大小确定(半径为R),点P的位置确定(OP等于d),则可得到PA·PB=r2-d2(是一个定值);如果点在圆外,也能得到PA·PB=d2-r2。在这样的基础上,给学生总结出圆幂定理,即:过一定点P向⊙O作任一直线,交⊙O于两点,则自定点P到两交点的两条线段之积为常数![]() (其中R为⊙O的半径),所以以上几个定理,统称为圆幂定理。
(其中R为⊙O的半径),所以以上几个定理,统称为圆幂定理。

三、运用几何画板进行题组教学,优化解题过程
以四边形各边的中点为顶点的四边形称为中点四边形,课本中有:求证任意四边形的中点四边形是平行四边形的例题。如下图:
(一) 在几何画板里,拖动点四边形的顶点A,改变四边形的形状和大小,从图形上面的度量值都可以得到,四边形的两组对边都相等。从而可以得到任意四边形的中点四边形是平行四边形。
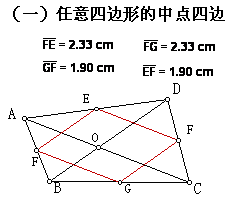

(二)在上图中,改变AC和BD的长度,使AC=BD,则可得到对角线相等的中点四边形是菱形
(三)在任意四边形的中点四边形的图形中,改变AC和BD的位置关系,使AC⊥BD,则可得到对角线相等的中点四边形是矩形。

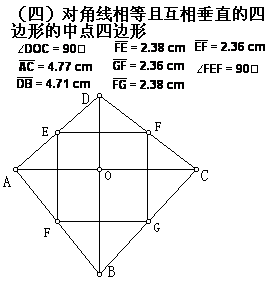
(四)如果在上图中,保持AC和BD的垂直关系,并使AC=BD,则可得到,对角线相等且互相垂直的四边形的中点四边形是正方形。
先前教学时,我们也在黑板上画出这样几个图,既费时费劲,又只是静态地进行研究,其效果远远不如动态的黑板-----几何画板这样形象、直观。而且通过演示,学生很快知道中点四边形与原四边形的对角线是否互相平分无关,只与原四边形对角线的位置关系和数量关系有关。
四、运用几何画板进行演示,探导图形性质
布鲁纳认为“探索是数学教学的生命”。在利用“几何画板”探索图形性质的过程中,数形结合使人一目了然,发现规律是那样的自然流畅。学生们能作为课堂教学的真正主体参与学习过程,参与教学实践而从内心领悟到数学的真谛。这正是几何画板在数学教学中的魅力所在。研究函数图象的性质,特别是增减性,是教学中的难点,有了几何画板,我们就来看看它的作用。
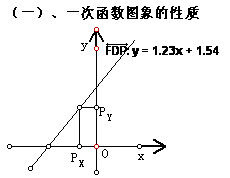
在坐标系内,任作一条直线,很容易得到它的解析式,我们拖动直线,就可以看到它的k和b在不断变化,学生们自己操作,仔细研究,就可以总结出,k、b大小与图象所经过的象限的关系。如下图,如果,拖动直线上的点P,则它的横坐标和纵坐标都在同时变化,当k>0和k<0,极易掌握它们的增减性。
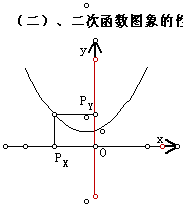
在研究二次函数图象的增减性时,我们拖动抛物线上点P,可以很形象地看到,y随着x的增大,一会儿增大,一会儿减小。问及同学们它的分界线在那里,再次研究金價后都能回答是抛物线的对称轴。
五、运用几何画板,展示运动变化的规律
平行四边形与特殊的四边形之间关系,有必然的联系,也有明显的区别。要弄清楚它们之间的关系,借助于几何画板,则一目了然。
(一)、在几何画板里,先画一个平行四边形,然后拖动顶点A,改变它的形状,从图上方的度量值可以发现,AC和BD的长度在不断变化,但AC和BD总是互相平分的。
(二) 在上图中,如果继续拖动顶点A,使∠DAB=90o,则可以得到,矩形的对角线相等且互相平分。

(三)如果拖动点A,使AD=AB,则可得到菱形的对角线互相垂直平分的性质。
(四)在上题中,使∠DAB=90o,则又可得到正方形的对角线相等且互相平分的性质。
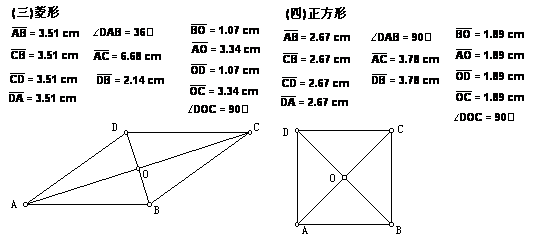
不管平行四边形发生怎样的变化,它的两条对边之间的数量关系和位置关系没有发生变化,对角之间的相等关系也没有发生变化,变化的是对角线之间的位置关系和数量关系发生了变化。
当然,几何画板在数学教学中作用,绝非仅此,不过从上面的几个例子中,可以看到,几何画板的动态性,让学生获得真正的数学经验,而不是数学结论。如果我们能把它作为学生的认知工具,学生的负担就减轻了。