初中数学新课程标准的实施使初中数学教学更紧密的与生产实践联系起来了，它彻底改变了传统的说教模式，更注重让学生在生产实践的大背景中学习数学知识，注重培养学生应用所学的数学知识解决实际问题的能力，教学形式也变得灵活多样，尤其是数学活动课的开展，给初中数学教学注入了勃勃生机，使数学的教与学变成了一种乐趣，教、学的效果明显增强。
一、 活动课的意义与分类
活动课是在教师的指导或参与下，学生充分发挥自主性，自己动手、动脑进行实践的过程，它是一种培养学生兴趣、发展能力的实践性教学活动；与学科教学一样，它也有明确的目的性，不同与简单的游戏与玩乐。数学活动课可以分为两类，一类是在教室进行的课堂动手、讨论、同学之间互动学习，有时还可以利用多媒体工具进行辅助教学，常用的数学软件有几何画板、PowerPoint、Excel等；另一类是在教室外，可以依据教学实践的需要，在操场、工厂、野外等地方进行，我认为初中数学活动课应以培养学生学习数学的兴趣为前提，以应用问题为中心内容进行研究设计。
实施新课程标准后，新的初中数学教材更加注重了知识与生产实际的结合，绝大多数章节知识的引入都是以生活原型的姿态出现的，而且有些章节内容就必须要求学生进行活动，如七上人教版实验教材4.3节《调查“你是怎样处理废电池？”》，这节课的教学目标之一就是让学生在活动中培养收集数据、处理数据、说明问题的能力，所以必须让学生走出课堂，进行数学活动。
二、 初中数学活动课应与生活实际牵手，培养学生的应用意识
以前，不少高中数学教师抱怨初中数学教学对学生的应用意识培养不够，上了高中后，学生在解决应用型数学问题时力不从心，空间想象能力也不强。这其中原因虽很多，但初中数学教学的“空对空”，即未将所学知识放入生活的大环境中是一个重要原因，学生很难学得透，或不懂得“学”与“用”的结合。《数学课程标准》要求“激发学生的学习兴趣，向学生提供充分从事数学活动的机会，帮助他们在自主探索和合作交流的数学活动中掌握数学知识、技能，获得广泛的数学实践经验”，这说明数学的教学要求学生全身心的参与，动态进行。数学知识来源于生产实践，最终又作用于生产实践，它是人们生产、生活必不可少的工具。在进行数学活动课教学时，我们可以根据数学的知识特点，重视纯数学知识与数学应用的内在联系，进行教学各环节的设计，提高学生应用能力。
三、 初中数学应用问题成为数学活动课的中心
数学活动课是培养学生的动手能力、创新意识、应用能力的重要途径，进行数学活动课教学不仅能提高学生学习数学的兴趣，而且能整体提高学生分析问题、解决问题的能力，因此，在实施初中数学教学过程中，切入应用问题非常必要，其内容应以初中数学教材内容为基础，联系实际问题而确定，可概括为如下几种问题：
1、函数学应用问题
函数是初中数学的重点内容，也是较难理解的一块内容，一次函数、二次函数的应用题很多，如：求成本最低、用料最省、产量（面积）最大、造价最低等应用性问题常可归纳为函数最值问题，通过实际问题，建立函数模型，确立自变量的限制条件，运用数学方法解决，有时这类问题还与几何图形结合起来，考查学生的数形结合思想，这种题型几乎每年的中考都会出现。
例1：某农户想利用一只1350的墙角砌一直角梯形鸡舍，现有一批可砌10米长墙的砖块，试问BC为何值时才能使鸡舍面积最大。
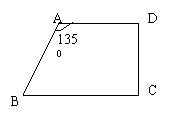
分析：本题可以设
，则
，再利用梯形的面积公式和几何知识，设梯形的面积为
，建立二次函数模型，找出
的取值范围，求函数的最大值即可解。
2、不等式的应用问题
初中阶段主要学习一元一次不等式，实际生活中的投资决策、最优化问题常用到不等式的知识。
例2：学生若干住若干宿舍，如果每间住4人，则还余19人；如果每间住6人，则有一间宿舍不空也不满，求有多少间宿舍和多少名学生？
分析：设有间宿舍，依题意，学生应有
人，当每间住6人时，假设全住满，则有
人，但是没有住满；当一个宿舍完全空出来时，只能住
人，肯定住不下，因此有了下列不等式：
，又因为人数为整数，所以可解出。
3、方程应用问题
① 打折问题
打折是生活中常见的商业行为，如何通过打折问题的教学，让学生了解打折的实质，增进对社会的了解，设置活动课教学，让学生亲身体验，加深学生对知识的理解是非常重要的。
例3：某商品因换季准备打折出售，如果按定价的七五折出售将赔25元，而按定价的九折出售将赚20元，问：这种商品定价多少？
② 方案问题
从多个方案中选取一个最优方案，考查学生对实际问题的判别能力。
例4：徐老师带团员若干到某地旅游，现有两个车主供选择，甲车主给出优惠条件是：学生9折，老师不收费；乙车主给出的优惠条件是包括老师在内，全部按8折优惠，若每张票价格是40元，那么乘哪家车比较合算？
③ 利率问题
存款、取款及贷款是生活中常见的，因此这类知识的应用也非常重要。
例5：为了准备你6年后上大学的学费10000元，你的父母现在就参加教育储蓄：⑴直接存一个6年期，年利率为2.28%，现在应存入本金多少元？⑵先存一个3年期，3年后将本息自动转存一个3年期，现在应存入本金多少元？(三年期年利率为2.70%)
④ 税收问题
照章纳税是每个公民应尽的责任，新教材中这是一个重要内容，有时它还与方程、函数相结合，考查学生的分类讨论思想。
例6：国家规定个发表文章、出版所获稿费应纳税，其计算方法是：⑴稿费不高于800元不纳税；⑵稿费高于800元，但不高于4000元应缴纳超过800元的那一部分的14%的税；⑶稿费高于4000元应缴纳全部稿费的11%的税。今知王教授出版一本著作获得一笔稿费，他缴纳了550元，那么王教授的这笔稿费是多少元？
⑤ 行程、工程问题
生活、生产中行程问题与工程问题最为常见，这类问题学生在小学已经接触，简单的问题都能解决，但到了初中后这类问题更加复杂，尤其与方程(组)相结合后，就整体考查学生的数学素质，是一类学生不容易掌握的问题。
例7：一只驳船，载重量是800吨，容积是795立方米，现装运铝合金和棉花，铝合金的比重是
吨/立方米，棉花的比重是0.25吨/立方米 ，问铝合金和棉花各装多少吨，才能充分利用船载重量和容积？
⑥ 浓度问题
浓度问题与物理化学联系紧密，属于跨学科应用问题，新的教学理念下，这类问题越来越得到重视，它要求学生在分析所给条件时，有充分的想象力与灵活运用多学科知识的能力。
例8：四种原料：⑴50%的酒精溶液150克，⑵90%的酒精溶液45克，⑶纯酒精45克，⑷水45克，请你设计一种方案，只取三种原料（各取若干或全量），配制成60%的酒精溶液200克，问你取哪三种原料？各取多少克？
分析：由题意，共有四种情况：⑴⑵⑶；⑴⑵⑷；⑴⑶⑷；⑵⑶⑷，但可排除⑴⑵⑶；⑴⑵⑷；⑵⑶⑷三种情况，因此只能选⑴⑶⑷。
解：设取纯酒精克，50%酒精溶液克，则：
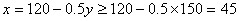
解得:
4、日历问题
日历是日常生活必需品，围绕它产生了不少数学问题，特别在新教材中，有一节对日历问题进行了较深入的讨论，它重点考查学生的观察能力。
5、数据的收集与整理
生活中每一个领域都离不开数据的收集与统计分析，这类问题在近几年的中考中出现的频率相当高，如2002年的转盘，抛硬币问题等。
6、几何知识应用
① 三角形与成比例线段
（相似）三角形是生活中常用到的几何图形之一，三角形相似的运用也相当广泛。
例9：要测量点B到池塘对岸A点的距离，选一点C，量得BC=50米，在BC上取CE=10米，再在AC上取一点D，使CD=
AC，又量得DE=16米，则AB间的距离为 米。
② 解直角三角形
生活中简单的测量，求解建筑物的高度，一般会用到解直角三角形的知识，其中还包含测量鉛價时的仰角、俯角。
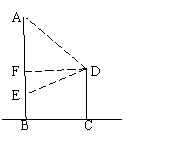
例10：如图，在甲建筑物上从A点到B点挂一长30米的宣传条幅，在乙建筑物顶部点D测得条幅顶端点A的仰角为450，底部点E的俯角为300，求底部不能到达的甲、乙两建筑物之间的水平距离BC。
③ 对称问题
让学生充分认识世界，认识图形，探索其中蕴含的几何规律。
例11：一牧童在A处牧马，A，B两地距河岸的距离AC,BD的长分别为700米和500米，且CD的距离是500米，天黑前牧童从A点将马牵到河边去饮水，再赶回家，那么，牧童至少要走多少米？
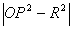
分析：本题要求学生能洞悉问题的本质，利用“两点之间线段最短”这一几何公理思考问题，并且用对称的思想进行解题。
④ 圆的问题
初中数学对圆的学习是比较深入的，教材详细的对弧、弧长、圆心角、圆周角的有关内容进行了讲述，学生重点学习了圆心角定理、圆周角定理、垂径定理，有些内容也融入了生活气息，如船能否过桥问题、船如何航行可绕过暗礁等。
例12：如图，阴影部分表示足球场上的门框，门框两端MN，恰好是圆一弦的两端，则A、B、C三点中， 点起脚射门进球希望最大，因为 。
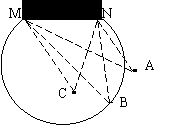
分析：本题主要是考查学生对圆周角
三个角的大小比较。
综上所述，与各类应用性问题相关的知识都是初中数学的重点内容，在设计数学活动课的教学内容时，我们可以从中选取某种类型或某个问题安排数学应用问题的学习。在数学活动课中，教师可以充分让学生去实践，从实践中获得知识，同时深刻掌握知识并有效地利用。所以利用数学活动课的优势，以应用性问题为中心，加强教学与实际的结合，激发学生的学习热情，培养学生的应用意识，提高学生的数学素质是初中数学教学所必不可少的。